Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
The Class 8 is an important year in a student’s life and Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 8 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete NCERT Class 8 Maths Book syllabus.

Q1. Identify the terms, their coefficients for each of the following expressions. (i) 5xyz2 – 3zy (ii) 1 + x + x2 (iii) 4x2 y2 – 4x2 y2 z2 + z2 (iv) 3 – pq + qr – p (v) (x/2) + (y/2) – xy (vi) 0.3a – 0.6ab + 0.5b
Solution :
| Sl. No. | Expression | Term | Coefficient |
| i) | 5xyz2 – 3zy |
Term: 5xyz
2
Term: -3zy |
5 -3 |
| ii) | 1 + x + x2 |
Term: 1
Term: x Term: x2 |
1 1 1 |
| iii) | 4x2 y2 – 4x2 y2 z2 + z2 |
Term: 4
x2
y
2
Term: -4 x2 y 2 z 2 Term : z 2 |
4 -4 1 |
| iv) | 3 – pq + qr – p | Term : 3 -pq qr -p | 3 -1 1 -1 |
| v) | (x/2) + (y/2) – xy | Term : x/2 Y/2 -xy | ½ 1/2 -1 |
| vi) | 0.3a – 0.6ab + 0.5b | Term : 0.3a -0.6ab 0.5b | 0.3 -0.6 0.5 |
2. Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories? x + y, 1000, x + x2 + x3 + x4 , 7 + y + 5x, 2y – 3y2 , 2y – 3y2 + 4y3 , 5x – 4y + 3xy, 4z – 15z2 , ab + bc + cd + da, pqr, p2 q + pq2 , 2p + 2q
Solution:
Let us first define the classifications of these 3 polynomials:
Monomials contain only one term.
Binomials contain only two terms.
Trinomials contain only three terms.
| x + y | two terms | Binomial |
| 1000 | one term | Monomial |
| x + x2 + x3 + x4 | four terms | Polynomial, and it does not fit in the listed three categories |
| 2y – 3y2 | two terms | Binomial |
| 2y – 3y2 + 4y 3 | three terms | Trinomial |
| 5x – 4y + 3xy | three terms | Trinomial |
| 4z – 15z 2 | two terms | Binomial |
| ab + bc + cd + da | four terms | Polynomial, and it does not fit in the listed three categories |
| pqr | one term | Monomial |
| p2 q + pq2 | two terms | Binomial |
| 2p + 2q | two terms | Binomial |
| 7 + y + 5x | three terms | Trinomial |
3. Add the following.
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p2 q2 – 3pq + 4, 5 + 7pq – 3p2 q2
(iv) l2 + m2 , m2 + n2 , n2 + l2 , 2lm + 2mn + 2nl
Solution:
i) (ab – bc) + (bc – ca) + (ca-ab)
= ab – bc + bc – ca + ca – ab
= ab – ab – bc + bc – ca + ca
= 0
ii) (a – b + ab) + (b – c + bc) + (c – a + ac)
= a – b + ab + b – c + bc + c – a + ac
= a – a +b – b +c – c + ab + bc + ca
= 0 + 0 + 0 + ab + bc + ca
= ab + bc + ca
iii) 2p2 q 2 – 3pq + 4, 5 + 7pq – 3p2 q2
= (2p2 q2 – 3pq + 4) + (5 + 7pq – 3p2 q2 )
= 2p2 q2 – 3p2 q2 – 3pq + 7pq + 4 + 5
= – p2 q2 + 4pq + 9
iv) (l2 + m2 ) + (m2 + n2 ) + (n2 + l2 ) + (2lm + 2mn + 2nl)
= l2 + l2 + m2 + m2 + n2 + n2 + 2lm + 2mn + 2nl
= 2l2 + 2m2 + 2n2 + 2lm + 2mn + 2nl
4. (a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p2 q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2 q
Solution:
(a) (12a – 9ab + 5b – 3) – (4a – 7ab + 3b + 12)
= 12a – 9ab + 5b – 3 – 4a + 7ab – 3b – 12
= 12a – 4a -9ab + 7ab +5b – 3b -3 -12
= 8a – 2ab + 2b – 15
b) (5xy – 2yz – 2zx + 10xyz) – (3xy + 5yz – 7zx)
= 5xy – 2yz – 2zx + 10xyz – 3xy – 5yz + 7zx
=5xy – 3xy – 2yz – 5yz – 2zx + 7zx + 10xyz
= 2xy – 7yz + 5zx + 10xyz
c) (18 – 3p – 11q + 5pq – 2pq2 + 5p2 q) – (4p2 q – 3pq + 5pq2 – 8p + 7q – 10)
= 18 – 3p – 11q + 5pq – 2pq2 + 5p2 q – 4p2 q + 3pq – 5pq2 + 8p – 7q + 10
=18+10 -3p+8p -11q – 7q + 5 pq+ 3pq- 2pq^2 – 5pq^2 + 5 p^2 q – 4p^2 q
= 28 + 5p – 18q + 8pq – 7pq2 + p2 q
1. Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) – 4p, 7p
(iii) – 4p, 7pq
(iv) 4p3 , – 3p
(v) 4p, 0
Solution:
(i) 4 , 7 p = 4 × 7 × p = 28p
(ii) – 4p × 7p = (-4 × 7 ) × (p × p )= -28p2
(iii) – 4p × 7pq =(-4 × 7 ) (p × pq) = -28p2 q
(iv) 4p3 × – 3p = (4 × -3 ) (p3 × p ) = -12p4
(v) 4p × 0 = 0
2. Find the areas of rectangles with the following pairs of monomials as their lengths and breadths, respectively.
(p, q) ; (10m, 5n) ; (20x2 , 5y2 ) ; (4x, 3x2 ) ; (3mn, 4np)
Solution:
Area of rectangle = Length x breadth. So, it is multiplication of two monomials.
The results can be written in square units.
(i) p ×q = pq
(ii)10m × 5n = 50mn
(iii) 20x2 × 5y2 = 100x2 y2
(iv) 4x × 3x2 = 12x3
(v) 3mn × 4np = 12mn2 p
3. Complete the following table of products:
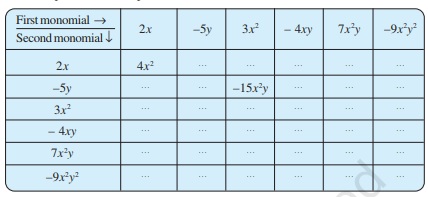
Solution:
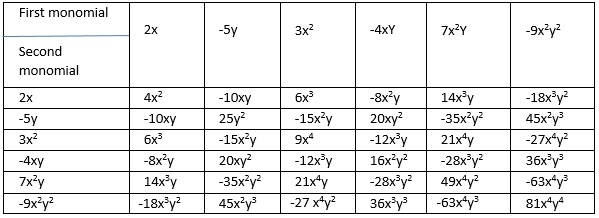
4. Obtain the volume of rectangular boxes with the following length, breadth and height, respectively.
(i) 5a, 3a2 , 7a 4
(ii)2p, 4q, 8r
(iii) xy, 2x2 y, 2xy 2
(iv)a, 2b, 3c
Solution:
Volume of rectangle = length x breadth x height. To evaluate volume of rectangular boxes, multiply all the monomials.
(i) 5a x 3a 2 x 7a 4 = (5 × 3 × 7) (a × a 2 × a 4 ) = 105a7
(ii) 2p x 4q x 8r = (2 × 4 × 8 ) (p × q × r ) = 64pqr
(iii) y × 2x2 y × 2xy 2 =(1 × 2 × 2 )( x × x2 × x × y × y × y 2 ) = 4x4 y4
(iv) a x2b x3c = (1 × 2 × 3 ) (a × b × c) = 6abc
5. Obtain the product of
(i) xy, yz, zx
(ii) a, – a2 , a3
(iii) 2, 4y, 8y2 , 16y3
(iv) a, 2b, 3c, 6abc
(v) m, – mn, mnp
Solution:
(i) xy × yz × zx = x2 y 2 z 2
(ii) a × – a2 × a3 = – a6
(iii) 2 × 4y × 8y2 × 16y3 = 1024 y6
(iv) a × 2b × 3c × 6abc = 36a2 b2 c2
(v) m × – mn × mnp = –m3 n2 p
1. Carry out the multiplication of the expressions in each of the following pairs.
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a²b²
(iv) a2 – 9, 4a
(v) pq + qr + rp, 0
Solution :
(i)4p(q + r) = 4pq + 4pr
(ii)ab(a – b) = a2 b – a b2
(iii)(a + b) (7a2 b2 ) = 7a3 b2 + 7a2 b3
(iv) (a2 – 9)(4a) = 4a3 – 36a
(v) (pq + qr + rp) × 0 = 0 ( Anything multiplied by zero is zero )
2. Complete the table.
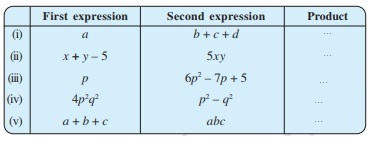
Solution:
| First expression | Second expression | Product | |
| (i) | a | b + c + d |
a(b+c+d)
= a×b + a×c + a×d = ab + ac + ad |
| (ii) | x + y – 5 | 5xy |
5 xy (x + y – 5)
= 5 xy x x + 5 xy x y – 5 xy x 5 = 5 x2 y + 5 xy2 – 25xy |
| (iii) | p | 6p2 – 7p + 5 |
p (6 p 2
-7 p +5)
= p× 6 p2 – p× 7 p + p×5 = 6 p3 – 7 p2 + 5 p |
| (iv) | 4 p2 q2 | P2 – q2 |
4p2
q2
* (p2
– q2
)
=4 p4 q2 – 4p2 q4 |
| (v) | a + b + c | abc |
abc(a + b + c)
= abc × a + abc × b + abc × c = a2 bc + ab2 c + abc2 |
3. Find the product.
i) a2 x (2a22 ) x (4a26 )
ii) (2/3 xy) ×(-9/10 x2 y2 )
(iii) (-10/3 pq3 /) × (6/5 p3 q)
(iv) (x) × (x2 ) × (x3 ) × (x4 )
Solution:
i) a2 x (2a22 ) x (4a26 )
= (2 × 4) ( a2 × a22 × a26 )
= 8 × a2 + 22 + 26
= 8a50
ii) (2xy/3) ×(-9x2 y2 /10)
=(2/3 × -9/10 ) ( x × x2 × y × y2 )
= (-3/5 x3 y3 )
iii) (-10pq3 /3) ×(6p3 q/5)
= ( -10/3 × 6/5 ) (p × p3 × q3 × q)
= (-4p4 q4 )
iv) ( x) x (x2 ) x (x3 ) x (x4 )
= x1 + 2 + 3 + 4
= x10
4. (a) Simplify 3x (4x – 5) + 3 and find its values for (i) x = 3 (ii) x =1/2
(b) Simplify a (a2 + a + 1) + 5 and find its value for (i) a = 0 , (ii) a = 1 (iii) a = – 1 .
Solution:
a) 3x (4x – 5) + 3
=3x ( 4x) – 3x( 5) +3
=12x2 – 15x + 3
(i) Putting x=3 in the equation we gets 12x2 – 15x + 3 =12(32 ) – 15 (3) +3
= 108 – 45 + 3
= 66
(ii) Putting x=1/2 in the equation we get
12x2 – 15x + 3 = 12 (1/2)2 – 15 (1/2) + 3
= 12 (1/4) – 15/2 +3
= 3 – 15/2 + 3
= 6- 15/2
= (12- 15 ) /2
= -3/2
b) a(a2 +a +1)+5
= a x a2 + a x a + a x 1 + 5 =a3 +a2 +a+ 5
(i) putting a=0 in the equation we get 03 +02 +0+5=5
(ii) putting a=1 in the equation we get 13 + 12 + 1+5 = 1 + 1 + 1+5 = 8
(iii) Putting a = -1 in the equation we get (-1)3 +(-1)2 + (-1)+5 = -1 + 1 – 1+5 = 4
5. (a) Add: p ( p – q), q ( q – r) and r ( r – p)
(b) Add: 2x (z – x – y) and 2y (z – y – x)
(c) Subtract: 3l (l – 4 m + 5 n) from 4l ( 10 n – 3 m + 2 l )
(d) Subtract: 3a (a + b + c ) – 2 b (a – b + c) from 4c ( – a + b + c )
Solution:
a) p ( p – q) + q ( q – r) + r ( r – p)
= (p2 – pq) + (q2 – qr) + (r2 – pr)
= p2 + q2 + r2 – pq – qr – pr
b) 2x (z – x – y) + 2y (z – y – x)
= (2xz – 2x2 – 2xy) + (2yz – 2y2 – 2xy)
= 2xz – 4xy + 2yz – 2x2 – 2y2
c) 4l ( 10 n – 3 m + 2 l ) – 3l (l – 4 m + 5 n)
= (40ln – 12lm + 8l2 ) – (3l2 – 12lm + 15ln)
= 40ln – 12lm + 8l2 – 3l2 +12lm -15 ln
= 25 ln + 5l2
d) 4c ( – a + b + c ) – (3a (a + b + c ) – 2 b (a – b + c))
= (-4ac + 4bc + 4c2 ) – (3a2 + 3ab + 3ac – ( 2ab – 2b2 + 2bc ))
=-4ac + 4bc + 4c2 – (3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc)
= -4ac + 4bc + 4c2 – 3a2 – 3ab – 3ac +2ab – 2b2 + 2bc
= -7ac + 6bc + 4c2 – 3a2 – ab – 2b2
1. Multiply the binomials.
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q2 ) and (3pq – 2q2 )
(vi) (3/4 a2 + 3b2 ) and 4( a2 – 2/3 b2 )
Solution :
(i) (2x + 5)(4x – 3)
= 2x x 4x – 2x x 3 + 5 x 4x – 5 x 3
= 8x² – 6x + 20x -15
= 8x² + 14x -15
ii) ( y – 8)(3y – 4)
= y x 3y – 4y – 8 x 3y + 32
= 3y2 – 4y – 24y + 32
= 3y2 – 28y + 32
(iii) ( 2.5l– 0.5m)(2.5l + 0.5m)
= 2.5l x 2.5 l + 2.5l x 0.5m – 0.5m x 2.5l – 0.5m x 0.5m
= 6.25l2 + 1.25 lm – 1.25 lm – 0.25 m 2
= 6.25l2 – 0.25 m 2
iv) (a + 3b) (x + 5)
= ax + 5a + 3bx + 15b
v) (2pq + 3q2 ) (3pq – 2q2 )
= 2pq x 3pq – 2pq x 2q2 + 3q2 x 3pq – 3q2 x 2q2
= 6p2 q2 – 4pq3 + 9pq3 – 6q4
= 6p2 q2 + 5pq3 – 6q4
(vi) (3/4 a² + 3b² ) and 4( a² – 2/3 b² )
=(3/4 a² + 3b² ) x 4( a² – 2/3 b² )
=(3/4 a² + 3b² ) x (4a² – 8/3 b² )
=3/4 a² x (4a² – 8/3 b² ) + 3b² x (4a² – 8/3 b² )
=3/4 a² x 4a² -3/4 a² x 8/3 b² + 3b² x 4a² – 3b² x 8/3 b²
=3a4 – 2a² b² + 12 a² b² – 8b 4
= 3a4 + 10a² b² – 8b4
2. Find the product.
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x – y)
(iii) (a2 + b) (a + b2 )
(iv) (p2 – q2 ) (2p + q)
Solution:
(i) (5 – 2x) (3 + x)
= 5 (3 + x) – 2x (3 + x)
=15 + 5x – 6x – 2x2
= 15 – x -2 x 2
(ii) (x + 7y) (7x – y)
= x(7x-y) + 7y ( 7x-y)
=7x2 – xy + 49xy – 7y2
= 7x2 – 7y2 + 48xy
iii) (a2 + b) (a + b2 )
= a2 (a + b2 ) + b(a + b2 )
= a3 + a2 b2 + ab + b3
= a3 + b3 + a2 b2 + ab
iv) (p2 – q2 ) (2p + q)
= p2 (2p + q) – q2 (2p + q)
=2p3 + p2 q – 2pq2 – q3
= 2p3 – q3 + p2 q – 2pq2
3. Simplify.
(i) (x2 – 5) (x + 5) + 25
(ii) (a2 + 5) (b3 + 3) + 5
(iii)(t + s2 )(t2 – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
(v) (x + y)(2x + y) + (x + 2y)(x – y)
(vi) (x + y)(x2 – xy + y2 )
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c)(a + b – c)
Solution:
i) (x2 – 5) (x + 5) + 25
= x3 + 5x2 – 5x – 25 + 25
= x3 + 5x2 – 5x
ii) (a2 + 5) (b3 + 3) + 5
= a2 b3 + 3a2 + 5b3 + 15 + 5
= a2 b3 + 5b3 + 3a2 + 20
iii) (t + s2 )(t2 – s)
= t (t2 – s)+ s2 (t2 – s)
= t3 – st + s2 t2 – s3
= t3 – s3 – st + s2 t2
iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
= (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
=(ac – ad + bc – bd) + (ac + ad – bc – bd) + (2ac + 2bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= 4ac
v) (x + y)(2x + y) + (x + 2y)(x – y)
= 2x2 + xy + 2xy + y2 + x2 – xy + 2xy – 2y2
= 3x2 + 4xy – y2
vi) (x + y)(x2 – xy + y2 )
= x3 – x2 y + xy2 + x2 y – xy2 + y3
= x3 + y3
vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x2 + 6xy + 4.5x – 6xy – 16y2 – 12y – 4.5x + 12y = 2.25x2 – 16y2
viii) (a + b + c)(a + b – c)
= a2 + ab – ac + ab + b2 – bc + ac + bc – c2
= a2 + b2 – c2 + 2ab
1. Use a suitable identity to get each of the following products.
(i) (x + 3) (x + 3)
(ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)
(iv) (3a – 1/2)(3a – 1/2)
(v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (a2 + b2 ) (- a2 + b2 )
(vii) (6x – 7) (6x + 7)
(viii) (- a + c) (- a + c)
(ix) (1/2x + 3/4y) (1/2x + 3/4y)
(x) (7a – 9b) (7a – 9b)
Solution:
(i) (x + 3) (x + 3) = (x + 3)2
= x2 + 6x + 9
Using (a+b)2 = a2 + b2 + 2ab
ii) (2y + 5) (2y + 5) = (2y + 5)2
= 4y2 + 20y + 25
Using (a+b)2 = a2 + b2 + 2ab
iii) (2a – 7) (2a – 7) = (2a – 7)2
= 4a2 – 28a + 49
Using (a-b)2 = a2 + b2 – 2ab
iv) (3a – 1/2)(3a – 1/2) = (3a – 1/2)2
= 9a2 -3a+(1/4)
Using (a-b)2 = a2 + b2 – 2ab
v) (1.1m – 0.4) (1.1m + 0.4)
= 1.21m2 – 0.16
Using (a – b)(a + b) = a2 – b2
vi) (a2 + b2 ) (– a2 + b2 )
= (b2 + a2 ) (b2 – a2 )
= -a4 + b4
Using (a – b)(a + b) = a2 – b2
vii) (6x – 7) (6x + 7)
=36x2 – 49
Using (a – b)(a + b) = a2 – b2
viii) (– a + c) (– a + c) = (– a + c)2
= c2 + a2 – 2ac
Using (a-b)2 = a2 + b2 – 2ab
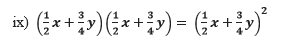
= (x2 /4) + (9y2 /16) + (3xy/4)
Using (a+b)2 = a2 + b2 + 2ab
x) (7a – 9b) (7a – 9b) = (7a – 9b)2
= 49a2 – 126ab + 81b2
Using (a-b)2 = a2 + b2 – 2ab
2. Use the identity (x + a) (x + b) = x2 + (a + b) x + ab to find the following products.
(i) (x + 3) (x + 7)
(ii) (4x + 5) (4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) (2a2 + 9) (2a2 + 5)
(vii) (xyz – 4) (xyz – 2)
Solution:
(i)(x + 3) (x + 7)
= x2 + (3+7)x + 21
= x2 + 10x + 21
ii) (4x + 5) (4x + 1)
= 16x2 + 4x + 20x + 5
= 16x2 + 24x + 5
iii) (4x – 5) (4x – 1)
= 16x2 – 4x – 20x + 5
= 16x2 – 24x + 5
iv) (4x + 5) (4x – 1)
= 16x2 + (5-1)4x – 5
= 16x2 +16x – 5
v) (2x + 5y) (2x + 3y)
= 4x2 + (5y + 3y)2x + 15y2
= 4x2 + 16xy + 15y2
vi) (2a2 + 9) (2a2 + 5)
= 4a4 + (9+5)2a2 + 45
= 4a4 + 28a2 + 45
vii) (xyz – 4) (xyz – 2)
= x2 y2 z2 + (-4 -2)xyz + 8
= x2 y2 z2 – 6xyz + 8
3. Find the following squares by using the identities.
(i) (b – 7)2
(ii) (xy + 3z)2
(iii) (6x2 – 5y)2
(iv) [(2m/3) + (3n/2)]2
(v) (0.4p – 0.5q)2
(vi) (2xy + 5y)2
Solution:
Using identities:
(a – b)2 = a2 + b2 – 2ab (a + b)2 = a2 + b2 + 2ab
(i) (b – 7)2 = b2 – 14b + 49
(ii) (xy + 3z)2 = x2 y2 + 6xyz + 9z2
(iii) (6x2 – 5y)2 = 36x4 – 60x2 y + 25y2
(iv) [(2m/3}) + (3n/2)]2 = (4m2 /9) +(9n2 /4) + 2mn
(v) (0.4p – 0.5q)2 = 0.16p2 – 0.4pq + 0.25q2
(vi) (2xy + 5y)2 = 4x2 y2 + 20xy2 + 25y2
4. Simplify.
(i) (a2 – b2 )2
(ii) (2x + 5)2 – (2x – 5)2
(iii) (7m – 8n)2 + (7m + 8n)2
(iv) (4m + 5n)2 + (5m + 4n)2
(v) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
(vi) (ab + bc)2 – 2ab²c
(vii) (m2 – n2 m)2 + 2m3 n2
Solution:
i) (a2 – b2 )2 = a4 + b4 – 2a2 b2
ii) (2x + 5)2
– (2x – 5)2
= 4x2
+ 20x + 25 – (4x2
– 20x + 25) = 4x2
+ 20x + 25 – 4x2
+ 20x – 25 = 40x
iii) (7m – 8n)2
+ (7m + 8n)2
= 49m2
– 112mn + 64n2
+ 49m2
+ 112mn + 64n2
= 98m2
+ 128n2
iv) (4m + 5n)2
+ (5m + 4n)2
= 16m2
+ 40mn + 25n2
+ 25m2
+ 40mn + 16n2
= 41m2
+ 80mn + 41n2
v) (2.5p – 1.5q)2
– (1.5p – 2.5q)2
= 6.25p2
– 7.5pq + 2.25q2
– 2.25p2
+ 7.5pq – 6.25q2
= 4p2
– 4q2
vi) (ab + bc)2 – 2ab²c = a2 b2 + 2ab2 c + b2 c2 – 2ab2 c = a2 b2 + b2 c2
vii) (m2
– n2
m)2
+ 2m3
n2
= m4
– 2m3
n2
+ m2
n4
+ 2m3
n2
= m4
+ m2
n4
5. Show that.
(i) (3x + 7)2 – 84x = (3x – 7)2
(ii) (9p – 5q)2 + 180pq = (9p + 5q)2
(iii) (4/3m – 3/4n)2 + 2mn = 16/9 m2 + 9/16 n2
(iv) (4pq + 3q)2 – (4pq – 3q)2 = 48pq2
(v) (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
Solution:
i) LHS = (3x + 7)2 – 84x
= 9x2
+ 42x + 49 – 84x
= 9x2
– 42x + 49
= RHS
LHS = RHS
ii) LHS = (9p – 5q)2
+ 180pq
= 81p2
– 90pq + 25q2
+ 180pq
= 81p2
+ 90pq + 25q2
RHS = (9p + 5q)2
= 81p2
+ 90pq + 25q2
LHS = RHS
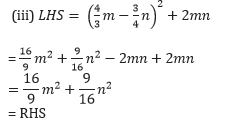
LHS = RHS
iv) LHS = (4pq + 3q)2 – (4pq – 3q)2
= 16p2 q2 + 24pq2 + 9q2 – 16p2 q2 + 24pq2 – 9q2
= 48pq2
= RHS
LHS = RHS
v) LHS = (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a)
= a2 – b2 + b2 – c2 + c2 – a2
= 0
= RHS
6. Using identities, evaluate.
(i) 71²
(ii) 99²
(iii) 1022
(iv) 998²
(v) 5.2²
(vi) 297 x 303
(vii) 78 x 82
(viii) 8.92
(ix) 10.5 x 9.5
Solution:
i) 712
= (70+1)2
= 702 + 140 + 12
= 4900 + 140 +1
= 5041
ii) 99²
= (100 -1)2
= 1002 – 200 + 12
= 10000 – 200 + 1
= 9801
iii) 1022
= (100 + 2)2
= 1002 + 400 + 22
= 10000 + 400 + 4 = 10404
iv) 9982
= (1000 – 2)2
= 10002 – 4000 + 22
= 1000000 – 4000 + 4
= 996004
v) 5.22
= (5 + 0.2)2
= 52 + 2 + 0.22
= 25 + 2 + 0.04 = 27.04
vi) 297 x 303
= (300 – 3 )(300 + 3)
= 3002 – 32
= 90000 – 9
= 89991
vii) 78 x 82
= (80 – 2)(80 + 2)
= 802 – 22
= 6400 – 4
= 6396
viii) 8.92
= (9 – 0.1)2
= 92 – 1.8 + 0.12
= 81 – 1.8 + 0.01
= 79.21
ix) 10.5 x 9.5
= (10 + 0.5)(10 – 0.5)
= 102 – 0.52
= 100 – 0.25
= 99.75
7. Using a2 – b2 = (a + b) (a – b), find
(i) 512 – 492
(ii) (1.02)2 – (0.98)2
(iii) 1532 – 1472
(iv) 12.12 – 7.92
Solution:
i) 512 – 492
= (51 + 49)(51 – 49) = 100 x 2 = 200
ii) (1.02)2 – (0.98)2
= (1.02 + 0.98)(1.02 – 0.98) = 2 x 0.04 = 0.08
iii) 1532 – 1472
= (153 + 147)(153 – 147) = 300 x 6 = 1800
iv) 12.12 – 7.92
= (12.1 + 7.9)(12.1 – 7.9) = 20 x 4.2= 84
8. Using (x + a) (x + b) = x2 + (a + b) x + ab, find
(i) 103 x 104
(ii) 5.1 x 5.2
(iii) 103 x 98
(iv) 9.7 x 9.8
Solution:
i) 103 x 104
= (100 + 3)(100 + 4)
= 1002 + (3 + 4)100 + 12
= 10000 + 700 + 12
= 10712
ii) 5.1 x 5.2
= (5 + 0.1)(5 + 0.2)
= 52 + (0.1 + 0.2)5 + 0.1 x 0.2
= 25 + 1.5 + 0.02
= 26.52
iii) 103 x 98
= (100 + 3)(100 – 2)
= 1002 + (3-2)100 – 6
= 10000 + 100 – 6
= 10094
iv) 9.7 x 9.8
= (9 + 0.7 )(9 + 0.8)
= 92 + (0.7 + 0.8)9 + 0.56
= 81 + 13.5 + 0.56
= 95.06
NCERT Solutions for Class 8 Maths Chapter 9 is mainly about the study of solving polynomial-related problems. The chapter builds a strong foundation for the students to deal with higher grade Maths problems.
Students can utilise the NCERT Solutions for Class 8 Maths Chapter 9 for any quick references to comprehend and solve complex problems.